A little while back I was involved in a casual conversation. As they often do, this one led to a reference of a specific Phish song. Our next logical step was to attempt to listen to said song. Unfortunately, despite a fairly large category of Phish shows, this specific song was not in the library. We had no internet connectivity, so we were left only what was in the catalog for the rest of the night.
This led to an inevitable question: What is the list of shows necessary for you to have at least one copy of every song?
Many people would simply walk away from that night never knowing the answer. I couldn’t help but give it a shot.
The Problem
To reiterate the problem: Find the shortest list of Phish shows that would contain at least one of every song.
Fortunately this is a problem that can be broken down to several, more manageable tasks. Or at least I had thought so, but I’ll get to that later. The most obvious steps were to:
- Get a list of every Phish song
- For each song, find the list of shows where that song was played
- For each show, find the setlist
- Find the shortest list of shows that contains every song
Of course, I underestimated the magnitude of the factorial function. That essentially rendered #4 impossible to solve, but I’m getting ahead of myself.
Getting the list of every song
I’m not accustomed to writing web scrapers, so I was hoping there’d be some API to the Phish.net database. They do have an API, but it seems to be for web developers through Javascript. After poking around there a little bit, I decided I’d have to go a more traditional route and go the scraper route. Fortunately with programming, a lot of the time you can simply use someone else’s code and start from there.
jsoup
I found jsoup, a Java HTML parser. This seemed to fit all of my needs. First, it has an online interface where you can test code without having to implement everything up front. Second, its free to use!
So you can simply tell jsoup to pull the source from any website. Since we’re looking for a list of every song Phish has played, the most obvious (and convenient) site to use was http://phish.net/songs. This gives the screenshot below, where the input and parsed output give clues as to what you’d be looking for.
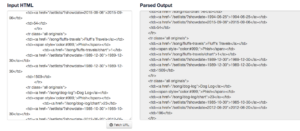
CSS Queries
If my aversion to web development hasn’t been obvious, it will start to become clear here. jsoup allows CSS Queries. I haven’t ever used CSS, but due to the user-friendliness of jsoup, I was able to quickly test queries. With a little intuition and some luck, I figured out that every song I wanted to look at was given the following line:
<tr class="all originals">
Assuing I’m only interested in originals, then I can use the CSS query of .originals in order to filter out everything that I don’t need.

Now I feel I’m getting close! I have been able to isolate the songs tagged as “originals” by the Phish.net folks. However, all of the additional links seem to muddy up the data – I don’t need to know “Alumni Blues Phish 106 1985-03-16 2016-07-20 29” I simply want “Alumni Blues”. A little more tinkering with CSS queries and I came across the “:first-of-type” argument. If I pull the first link (HTML type a) I get what I want.

Halfway there!
Java Implementation
Now that I have everything working form the web interface, it’s time to look into the Java implementation. Essentially two magical lines of code will be able to pull an entire page and filter out the necessary “elements”.
Document document = Jsoup.connect("http://phish.net/songs").get();
Elements elements = document.select(".originals :first-of-type a");
With those two lines, there’s an object elements that can be used to loop over every song on the site! With three more lines of code (and two more classes that I won’t discuss) the entire list of songs can be created.
for (Element element : elements) {
Song song = new Song(element.text(), "http://www.phish.net/" + element.attr("href"));
songList.add(song);
}After all that, we have a list of song names and, more importantly, URLs to information about the song.
Getting the rest of the data
I had alluded that the important part of the list of songs was actually the URL of the song. Using the same jsoup example from above, only instead of searching for the “.originals” class, the “.etpitem” is needed. With a little more code, you’ll end up with a list of all shows and using the “.setlist-song” class you’ll be able to pull all songs from every show.
After all of this, with a little bit of Java trickery, all the data can wrapped up in a couple of lists. This can be visualized by a simple mapping image.

Each song would be in the left box. Each arrow coming off each song indicates that song has been played in specific shows. The list of shows would be in the right box, and the arrows leading into them could be thought of the show’s setlist.
At this point everything related to scraping and organization is complete. The only thing left to do is simply solve the “minimum show list” that covers all of the songs.
The Algorithm
Recursion
In a lot of these projects I find myself leaning toward recursion whenever I can. Since I’ve been in the embedded world most of my career, I feel like recursion is often bad practice (if not explicitly forbidden.) This offered an interesting problem where a recursive brute-force method made sense…
Or so I thought…
The logic of the algorithm can be seen in the flowchart below. Not the best flowchart I’ve made, but deal with it. Hopefully the link stays active after my 1-week gliffy trial expires.

There were a couple of intuitive tricks that I had used in this algorithm to help speed things up.
Early Exit
Near the top of the flowchart, I have what I called “Early Exit.” It is essentially a simple check to see if the number of songs left is possible to be covered by the number of shows left. For instance, if I have 100 songs left and only 2 shows left, I know that I won’t be able to cover all of those songs since Phish only played about 15-20 songs per show. In that case, I can exit the current processing stack. I called this an early exit, since I was able to kick out of the routine very “early” in the flowchart. Hopefully that’d speed up the selection algorithm quite quickly.
Sorted Selection
Another intuition I had was that I could start with songs that had been played only once or twice, and select those shows first. That is part of the “Least Played” part of the “Find Least Played, Unselected Song” step. Essentially if a song was only played once, it has to be in the minimum list of shows. So let’s select that show first. That way we don’t have to loop through the 597 times (at the time of writing this) that You Enjoy Myself has been played.
Code
The code to do all of this was probably easier to make than the Gliffy flowchart:
private static boolean chooseShow(final int numShowsToSelect) {
boolean rval = false;
// Check if we can exit early
if (numShowsToSelect * maxSongsPerShow < numSongsLeftToSelect) {
return false;
}
Song nextUnplayedSong = SongUtils.getNextUnplayedSong(songList);
if (nextUnplayedSong == null) {
// The "we're done" return
return true;
} else {
List currentShowList = nextUnplayedSong.getShowList();
for (Show currentShow : currentShowList) {
int numSongsAdded = currentShow.select();
numSongsLeftToSelect -= numSongsAdded;
if ( numSongsLeftToSelect == 0
|| chooseShow(numShowsToSelect - 1)) {
return true;
} else {
int numSongsRemoved = currentShow.unselect();
numSongsLeftToSelect += numSongsRemoved;
}
}
}
return false;
}
for (int numShowsToSelect = 1; numShowsToSelect < songList.size(); numShowsToSelect++) {
long startTime = System.nanoTime();
if (chooseShow(numShowsToSelect)) {
// Success!
System.out.println("Successfully got it with " + numShowsToSelect + " shows!");
break;
}
long endTime = System.nanoTime();
long duration = endTime - startTime;
System.out.println("Tried with " + numShowsToSelect + " shows - took: " + (duration / 1000000000.0) + " seconds");
}Result
Nope.
By the time I hit 57 songs the algorithm was taking 20,000 seconds and increasing by a factor of 5 with every iteration. As it turns out, small numbers can become really, really big. There are about 10 million concert combinations with songs that were only played 5 times. And there are only 10 songs that were only played 5 times. In a true brute-force search, each of those had to be considered. Next.
Breadth First Search
For some reason, I had thought that the Breadth First Search (BFS) would have solved my issues from the recursive strategy. The reason being that each time I had to go “one deeper” the algorithm basically had to start over from scratch. This is a benefit of the BFS: It remembers the stack of operations that got you there, so that all you have to do is add each step to the processing queue. Wikipedia has a good enough explanation of BFS, so I’ll leave that as an exercise to the reader.
To explain this in further detail, I describe the final logic of the recursive algorithm as such:
- Go to the next “Show”
- Select each song from the show (add 1 to the play count)
- If every song is selected, we’re done
- If every song is not selected, unselect each song from the show
It can be see that we have to loop through each song, for each show. Not good! However, only one copy of the SongList is kept in memory, with their counts updated.
In the case of BFS, we’re using a processing queue. This means that every time we want to consider a new show, we have to copy the entire song and selected show arrays. So essentially the logic is:
- Pop the next Show and UnplayedSongList off the Execution Queue
- Remove each song played at the show from the UnplayedSongList
- If the UnplayedSongList is empty, we’re done!
- If the UnplayedSongList is not empty:
- Find the next unplayed song
- Add a copy of the UnplayedSongList and the next Show to the end of the Execution Queue
This led to a LOT of memory usage, since I had to make a copy of each selectedShowList, nextShow, and unplayedSongList for every show permutation. Further, the lookup from Show to Song was VERY quick in the recursive search method. Since these are copies of objects and not the objects themselves, there has to be an actual search for each song. NOTE: This could be done in O(logn), but even that is worse than O(1).
Long and the short of it
The recursive algorithm seemed to be much better than the BFS in this instance. It didn’t seem to take up much memory, though there were two loops over each setlist to mark / clear each song.
The BFS could be optimized so that I’m not copying the entire song list (URL, title, etc.) but I’m not confident that’ll work out either. There are simply too many possibilities.
Greedy algorithm
Here’s the sure fire way to come up with “A Solution.” It essentially involves the same process as the Depth First Search algorithm, but instead of trying every combination, it selects the “best” show it can find. The algorithm can simply be outlined as:
- Find the song that has been been played the fewest times
- From that song, find the show that selects the most unplayed songs
- Select that show, and mark all those songs played
Doing this guarantees an answer (if the problem is solvable) but is not guaranteed to give the “best” answer.
Code
private static void doGreedyRoutine() {
Song nextUnplayedSong;
while ((nextUnplayedSong = SongUtils.getNextUnplayedSong(songList)) != null) {
List<Show> currentShowList = nextUnplayedSong.getShowList();
if (currentShowList == null) {
continue;
}
double showWeight = 0;
int optimalIndex = -1;
for (int i = 0; i < currentShowList.size(); i++) {
Show currentShow = currentShowList.get(i);
double tempShowWeight = currentShow.getShowWeight();
if (tempShowWeight > showWeight) {
showWeight = tempShowWeight;
optimalIndex = i;
}
}
if (optimalIndex > -1) {
Show selectedShow = currentShowList.get(optimalIndex);
selectedShow.select();
}
}
int i = 0;
for (Show showDisplay : showList) {
if (showDisplay.isSelected()) {
i++;
System.out.println(i + ". " + showDisplay.toString());
}
}
}
Results
We got something! The problem can be solved in at least 71 shows (as of the time I had scraped the Phish.net data)
This algorithm takes milliseconds to run, whereas the others took days and failed.
- http://www.phish.net//setlists/phish-december-30-1989-the-wetlands-preserve-new-york-ny-usa.html
- http://www.phish.net//setlists/phish-december-31-1999-big-cypress-seminole-indian-reservation-big-cypress-fl-usa.html
- http://www.phish.net//setlists/phish-july-24-1999-alpine-valley-music-theatre-east-troy-wi-usa.html
- http://www.phish.net//setlists/phish-august-11-2009-toyota-park-bridgeview-il-usa.html
- http://www.phish.net//setlists/phish-august-16-1996-plattsburgh-air-force-base-plattsburgh-ny-usa.html
- http://www.phish.net//setlists/phish-november-27-2009-times-union-center-albany-ny-usa.html
- http://www.phish.net//setlists/phish-march-04-1985-hunts-burlington-vt-usa.html
- http://www.phish.net//setlists/phish-march-17-1990-23-east-caberet-ardmore-pa-usa.html
- http://www.phish.net//setlists/phish-may-04-1990-the-colonial-theatre-keene-nh-usa.html
- http://www.phish.net//setlists/phish-august-02-2003-loring-commerce-centre-limestone-me-usa.html
- http://www.phish.net//setlists/phish-march-06-1987-goddard-college-plainfield-vt-usa.html
- http://www.phish.net//setlists/phish-april-24-1987-billings-lounge-university-of-vermont-burlington-vt-usa.html
- http://www.phish.net//setlists/phish-august-15-2004-newport-state-airport-coventry-vt-usa.html
- http://www.phish.net//setlists/phish-august-14-1997-darien-lake-performing-arts-center-darien-center-ny-usa.html
- http://www.phish.net//setlists/phish-august-17-1997-loring-commerce-centre-limestone-me-usa.html
- http://www.phish.net//setlists/phish-august-15-1998-loring-commerce-centre-limestone-me-usa.html
- http://www.phish.net//setlists/phish-october-17-1998-shoreline-amphitheatre-mountain-view-ca-usa.html
- http://www.phish.net//setlists/phish-may-09-1989-the-front-burlington-vt-usa.html
- http://www.phish.net//setlists/phish-october-26-1989-the-wetlands-preserve-new-york-ny-usa.html
- http://www.phish.net//setlists/phish-december-15-1995-corestates-spectrum-philadelphia-pa-usa.html
- http://www.phish.net//setlists/phish-june-15-2010-ntelos-pavilion-portsmouth-va-usa.html
- http://www.phish.net//setlists/phish-june-22-2010-comcast-center-mansfield-ma-usa.html
- http://www.phish.net//setlists/phish-july-02-2011-watkins-glen-international-watkins-glen-ny-usa.html
- http://www.phish.net//setlists/phish-october-31-2013-boardwalk-hall-atlantic-city-nj-usa.html
- http://www.phish.net//setlists/phish-october-31-2014-mgm-grand-garden-arena-las-vegas-nv-usa.html
- http://www.phish.net//setlists/phish-august-22-2015-watkins-glen-international-watkins-glen-ny-usa.html
- http://www.phish.net//setlists/phish-december-30-2015-madison-square-garden-new-york-ny-usa.html
- http://www.phish.net//setlists/phish-august-21-2015-watkins-glen-international-watkins-glen-ny-usa.html
- http://www.phish.net//setlists/phish-october-24-2016-verizon-theatre-at-grand-prairie-grand-prairie-tx-usa.html
- http://www.phish.net//setlists/phish-october-28-2016-mgm-grand-garden-arena-las-vegas-nv-usa.html
- http://www.phish.net//setlists/phish-april-22-1994-township-auditorium-columbia-sc-usa.html
- http://www.phish.net//setlists/phish-may-02-1992-cabaret-metro-chicago-il-usa.html
- http://www.phish.net//setlists/phish-april-18-1990-hermans-hideaway-denver-co-usa.html
- http://www.phish.net//setlists/phish-september-27-1985-slade-hall-university-of-vermont-burlington-vt-usa.html
- http://www.phish.net//setlists/phish-october-01-2000-desert-sky-pavilion-phoenix-az-usa.html
- http://www.phish.net//setlists/phish-june-06-1997-brad-sandss-and-pete-carinis-house-charlotte-vt-usa.html
- http://www.phish.net//setlists/phish-may-14-1995-fishs-house-burlington-vt-usa.html
- http://www.phish.net//setlists/phish-september-12-1988-sams-tavern-burlington-vt-usa.html
- http://www.phish.net//setlists/phish-october-11-2010-1stbank-center-broomfield-co-usa.html
- http://www.phish.net//setlists/phish-july-27-2013-gorge-amphitheatre-george-wa-usa.html
- http://www.phish.net//setlists/phish-june-29-2016-the-mann-center-for-the-performing-arts-philadelphia-pa-usa.html
- http://www.phish.net//setlists/phish-october-21-2016-verizon-wireless-amphitheatre-at-encore-park-alpharetta-ga-usa.html
- http://www.phish.net//setlists/phish-october-31-1991-armstrong-hall-colorado-college-colorado-springs-co-usa.html
- http://www.phish.net//setlists/phish-october-08-1990-the-bayou-washington-dc-usa.html
- http://www.phish.net//setlists/phish-july-17-1993-the-filene-center-at-wolf-trap-vienna-va-usa.html
- http://www.phish.net//setlists/phish-july-11-2000-deer-creek-music-center-noblesville-in-usa.html
- http://www.phish.net//setlists/phish-october-15-2010-north-charleston-coliseum-north-charleston-sc-usa.html
- http://www.phish.net//setlists/phish-december-28-2010-dcu-center-worcester-ma-usa.html
- http://www.phish.net//setlists/phish-december-29-2009-american-airlines-arena-miami-fl-usa.html
- http://www.phish.net//setlists/phish-april-20-1991-douglass-dining-center-university-of-rochester-rochester-ny-usa.html
- http://www.phish.net//setlists/phish-october-15-1986-hunts-burlington-vt-usa.html
- http://www.phish.net//setlists/phish-december-17-1999-hampton-coliseum-hampton-va-usa.html
- http://www.phish.net//setlists/phish-june-18-2010-the-comcast-theatre-hartford-ct-usa.html
- http://www.phish.net//setlists/phish-july-02-1998-the-grey-hall-freetown-christiania-copenhagen-denmark.html
- http://www.phish.net//setlists/phish-june-30-1999-sandstone-amphitheatre-bonner-springs-ks-usa.html
- http://www.phish.net//setlists/phish-june-24-2016-wrigley-field-chicago-il-usa.html
- http://www.phish.net//setlists/phish-may-14-1992-the-capitol-theatre-port-chester-ny-usa.html
- http://www.phish.net//setlists/phish-july-28-2015-austin360-amphitheater-del-valle-tx-usa.html
- http://www.phish.net//setlists/phish-february-16-2003-thomas-mack-center-las-vegas-nv-usa.html
- http://www.phish.net//setlists/phish-february-13-1997-shepherds-bush-empire-london-england.html
- http://www.phish.net//setlists/phish-november-13-1997-thomas-mack-center-las-vegas-nv-usa.html
- http://www.phish.net//setlists/phish-june-25-1994-nautica-stage-cleveland-oh-usa.html
- http://www.phish.net//setlists/phish-august-09-1987-nectars-burlington-vt-usa.html
- http://www.phish.net//setlists/phish-september-28-1995-summer-pops-embarcadero-center-san-diego-ca-usa.html
- http://www.phish.net//setlists/phish-march-30-1992-mississippi-nights-st-louis-mo-usa.html
- http://www.phish.net//setlists/phish-december-02-2003-fleetcenter-boston-ma-usa.html
- http://www.phish.net//setlists/phish-october-24-1995-dane-county-coliseum-madison-wi-usa.html
- http://www.phish.net//setlists/phish-december-29-2012-madison-square-garden-new-york-ny-usa.html
- http://www.phish.net//setlists/phish-november-23-1992-broome-county-forum-binghamton-ny-usa.html
- http://www.phish.net//setlists/phish-september-13-1990-the-wetlands-preserve-new-york-ny-usa.html
- http://www.phish.net//setlists/phish-april-04-1994-the-flynn-theatre-burlington-vt-usa.html
Next Steps
I’m saddened that I wasn’t able to get the “Absolute” solution down. I’m not yet convinced that it can’t be done, although I have done the math that suggests it probably can’t. That’ll be another post.
The next steps toward getting a better solution (I know for a fact that it can be done in fewer shows) are to REALLY optimize the search algorithm. This would mean running trials in parallel and trying to minimize the number of clock cycles per trial.
The final step would be to port the “optimized” code to an FPGA that has a lot of horsepower and see if a pipeline can be set up to really run through trials. Initial “Best Case Scenario” calculations suggest that it might take about 19 years of computing time, assuming one billion operations per second. So getting that down by a factor of hundreds is quite important. Could lead me to my first FPGA project…
